Мозаика Пенроуза и древние исламские узоры

В 1973 году английский математик Роджер Пенроуз (Roger Penrose) создал особенную мозаику из геометрических фигур, которая так и стала называться - мозаикой Пенроуза.
Мозаика Пенроуза представляет собой узор, собранный из многоугольных плиток двух определённых форм (немного различающихся ромбов). Ими можно замостить бесконечную плоскость без пробелов.

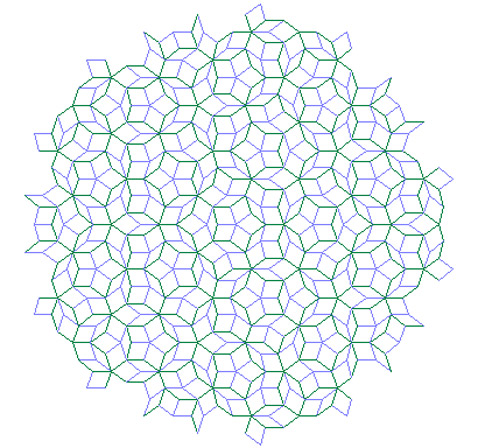
Мозаика Пенроуза в версии её создателя.
Она собрана из ромбов двух типов,
один – с углом 72 градуса, другой – с углом 36 градусов.
Картина получается симметричная, но не периодичная.

Получающееся изображение выглядит так, будто является неким "ритмическим" орнаментом – картинкой, обладающей трансляционной симметрией. Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно "копировать" на плоскости, а затем совмещать эти "дубликаты" друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).

Однако, если присмотреться, можно узреть, что в узоре Пенроуза нет таких повторяющихся структур – он апериодичен. Но дело отнюдь не в оптическом обмане, а в том, что мозаика не хаотична: она обладает вращательной симметрией пятого порядка.

Это значит, что изображение можно поворачивать на минимальный угол, равный 360 / n градусам, где n – порядок симметрии, в данном случае n = 5. Следовательно, угол поворота, который ничего не меняет, должен быть кратен 360 / 5 = 72 градусам.

Примерно десятилетие выдумка Пенроуза считалась не более чем милой математической абстракцией. Однако в 1984 году Дэн Шехтман (Dan Shechtman), профессор израильского технологического института (Technion), занимаясь изучением строения алюминиево-магниевого сплава, обнаружил, что на атомной решётке этого вещества происходит дифракция.

Предыдущие представления, существовавшие в физике твёрдого тела, исключали такую возможность: структура дифракционной картины обладает симметрией пятого порядка. Её части нельзя совмещать параллельным переносом, а значит, это вовсе никакой не кристалл. Но дифракция характерна как раз для кристаллической решётки! Учёные договорились о том, что данный вариант будет назваться квазикристаллами – чем-то вроде особого состояния вещества. Ну а вся красота открытия в том, что для него уже давно была готова математическая модель - мозаика Пенроуза.

А совсем недавно стало понятно, что этой математической конструкции намного больше лет, чем можно было себе представить. В 2007 году Питер Лу (Peter J. Lu), физик из Гарварда (Harvard University) за компанию с другим физиком — Полом Стейнхардтом (Paul J. Steinhardt), но из Принстона (Princeton University), — опубликовал в Science статью, посвящённую мозаикам Пенроуза . Казалось бы, неожиданного тут немного: открытие квазикристаллов привлекло живой интерес к данной теме, что привело к появлению кучи публикаций в научной прессе.

Однако изюминка работы в том, что она посвящена далеко не современной науке. Да и вообще — не науке. Питер Лу обратил внимание на узоры, покрывающие мечети в Азии, построенные ещё в Средневековье. Эти легко узнаваемые рисунки сделаны из мозаичной плитки. Они называются гирихи (от арабского слова "узел") и представляют собой геометрический орнамент, характерный для исламского искусства и состоящий из многоугольных фигур.

Образец выкладки плитки, показанный в арабском манускрипте XV века.
Цветами исследователи выделили повторяющиеся области.
На основе этих пяти элементов выстроены все геометрические узоры
средневековых арабских мастеров. Повторяющиеся элементы
не обязательно совпадают с границами плиток.

В исламском орнаменте выделяют два стиля: геометрический – гирих, и растительный – ислими.
Гирих (перс.) – сложный геометрический орнамент, составленный из стилизованных в прямоугольные и полигональные фигуры линий. В большинстве случаев используется для внешнего оформления мечетей и книг в крупном издании.
Ислими (перс.) – вид орнамента, построенного на соединении вьюнка и спирали. Воплощает в стилизованной или натуралистической форме идею непрерывно развивающегося цветущего лиственного побега и включает в себя бесконечное разнообразие вариантов. Наибольшее распространение он получил в одежде, книгах, внутренней отделке мечетей, посуде.

Обложка Корана 1306-1315 годов и прорисовка геометрических фрагментов,
на которых основан узор. Этот и следующий примеры не соответствуют
решёткам Пенроуза, но обладают вращательной симметрией пятого порядка

До открытия Питера Лу считалось, что древние архитекторы создавали узоры гириха c помощью линейки и циркуля (если вообще не по наитию). Однако пару лет назад, находясь во время путешествия в Узбекистане, Лу заинтересовался узорами мозаик, украшавшими местную средневековую архитектуру, и приметил в них что-то знакомое. Вернувшись в Гарвард, учёный стал рассматривать аналогичные мотивы в мозаиках на стенах средневековых построек Афганистана, Ирана, Ирака и Турции.

Этот образец датирован более поздним периодом – 1622 год (индийская мечеть).
Глядя на него и прорисовку его структуры, нельзя не восхититься трудолюбию
исследователей. И, конечно же, самих мастеров.

Питер Лу обнаружил, что геометрические схемы гирихов практически одинаковы, и смог выделить основные элементы, использовавшихся во всех геометрических орнаментах. Кроме того, он нашёл чертежи этих изображений в старинных манускриптах, которыми древние художники пользовались в качестве своеобразной шпаргалки по украшению стен.
Для создания этих узоров применяли не простые, случайно придуманные контуры, а фигуры, которые были расположены в определённом порядке. Древние узоры оказались точными построениями мозаик Пенроуза!

На этих снимках выделены одинаковые области,
хотя это и фотографии из самых разных мечетей

В исламской традиции существовал строгий запрет на изображение людей и животных, поэтому в оформлении зданий большую популярность приобрёл геометрический орнамент. Средневековые мастера умудрялись как-то делать его разнообразным. Но в чём был секрет их "стратегии" – никто не знал. Так вот, секрет как раз оказывается в использовании специальных мозаик, которые могут, оставаясь симметричными, заполнять плоскость, не повторяясь.

Другой "фокус" этих изображений в том, что, "копируя" такие схемы в различных храмах по чертежам, художники неизбежно должны были бы допустить искажения. Но нарушения данного характера минимальны. Объясняется это только тем, что в масштабных чертежах смысла не была: главное – принцип, по которому строить картину.

Для сборки гирихов применяли плитки пяти видов (десяти— и пятиугольные ромбы и "бабочки"), которые в мозаике составлялись, прилегая друг к другу без свободного пространства между ними. Мозаики созданные из них, могли обладать как сразу вращательной и трансляционной симметрией, так и только вращательной симметрией пятого порядка (то есть являлись мозаиками Пенроуза).

Фрагмент орнамента иранского мавзолея 1304 года. Справа – реконструкция гирихов

Исследовав сотни фотографий средневековых мусульманских достопримечательностей, Лу со Стейнхардтом смогли датировать появление подобной тенденции XIII веком. Постепенно этот способ приобретал всё большую популярность и к XV веку стал широко распространённым. Датировка примерно совпадает с периодом развития техники декорирования дворцов, мечетей, различных важных зданий глазурованной цветной керамической плиткой в форме различных многоугольников. То есть керамическую плитку специальных форм создавали именно для гирихов.

Образцом почти идеальной квазикристаллической структуры исследователи посчитали святилище имама Дарб-и в иранском городе Исфахане, датируемое 1453 годом.

Портал святилища имама Дарб-и в Исфахане (Иран).
Здесь друг на друга наложены сразу две системы гирихов.

Колонна внутреннего двора мечети в Турции (около 1200 года)
и стены медресе в Иране (1219 год). Это ранние произведения,
и в них используется всего два структурных элемента, найденных Лу

Теперь остается найти ответы на ряд загадок в истории гириха и мозаик Пенроуза. Каким образом и для чего древние математики открыли квазикристаллические структуры? Придавали ли средневековые арабы мозаикам какой-то иной смысл, кроме художественного? Почему столь интересная математическая концепция была забыта на полтысячелетия? И самое интересное - какие еще современные открытия являются новым, которое на самом деле - хорошо забытое старое?

Источник: membrana.ru

версия для печати

Следующая страница: Красота фракталов. Ю.Данилов